
关于变换的一些笔记。
2D Transformation
Scale
$$\begin{bmatrix} y'\\x' \end{bmatrix} = \begin{bmatrix} s_x & 0\\ 0 & s_y \end{bmatrix} \begin{bmatrix} x\\y \end{bmatrix}$$Reflection
$$\begin{bmatrix} x'\\y' \end{bmatrix} = \begin{bmatrix} -1 & 0\\ 0 & 1 \end{bmatrix} \begin{bmatrix} x\\y \end{bmatrix}$$Shear
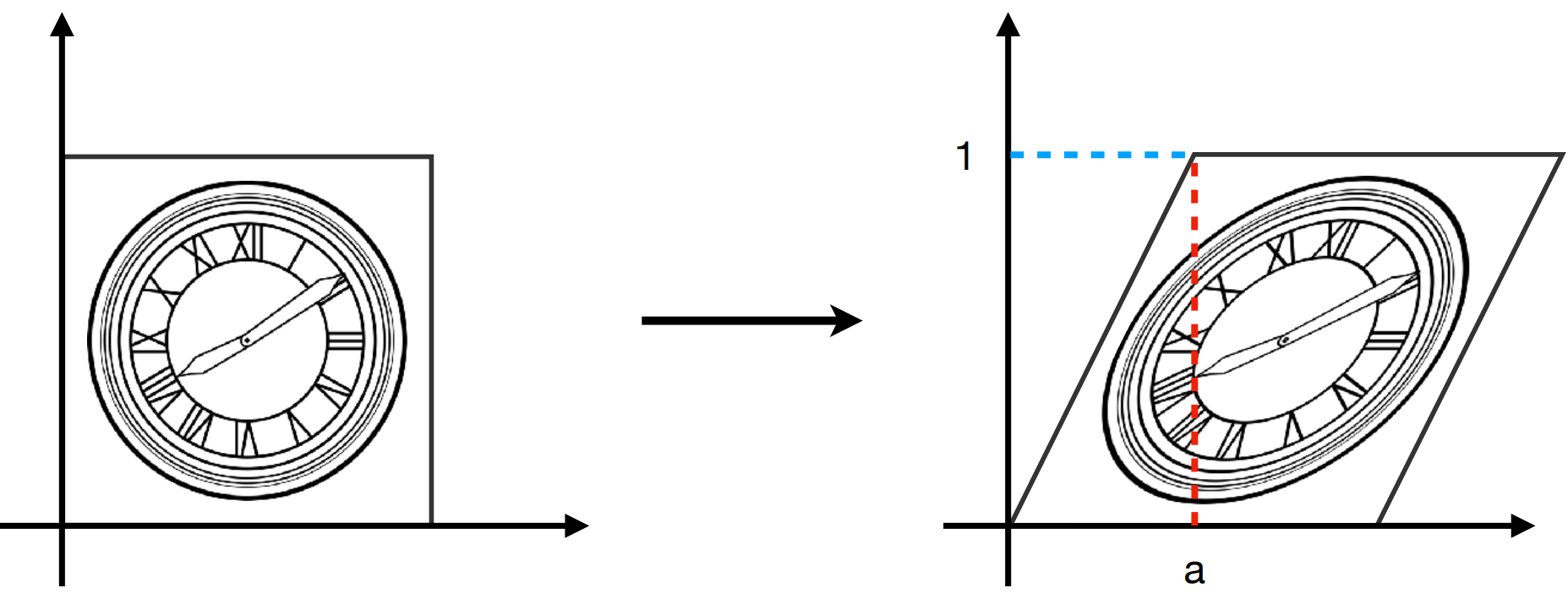
Rotate
一般默认为绕原点逆时针方向旋转
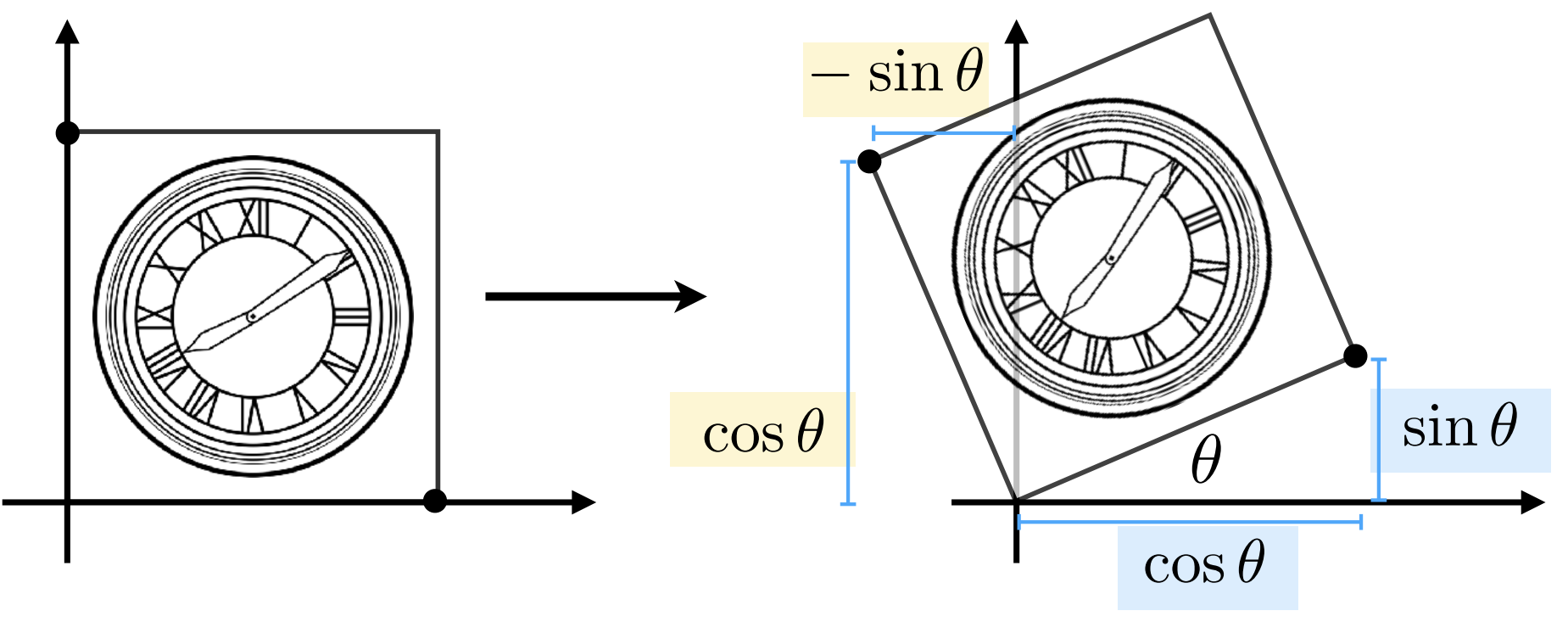
逆:$R ^ {-1}(\theta) = R(-\theta) = R ^ T(\theta)$
旋转矩阵是正交矩阵
Homogeneous Coordinates
Why
平移变换不能写成上述矩阵形式
$$\begin{bmatrix} x'\\y' \end{bmatrix} = \begin{bmatrix} a & b\\ c & d \end{bmatrix} \begin{bmatrix} x\\y \end{bmatrix} + \begin{bmatrix} t_x\\t_y \end{bmatrix}$$但是不想把平移作为一种特殊变换
- 2D Point = $(x, y, 1) ^ T$
- 2D vector = $(x, y, 0) ^ T$
向量具有平移不变性,$w = 0$
$$\begin{bmatrix} x'\\y'\\w' \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x\\ 0 & 1 & t_y\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\y\\1 \end{bmatrix} = \begin{bmatrix} x + t_x\\ y + t_y\\ 1 \end{bmatrix}$$扩充:$\begin{bmatrix}x\\y\\w\end{bmatrix}$ is the 2D point $\begin{bmatrix}x/w\\y/w\\1\end{bmatrix}, w \neq 0$
所以 point + point 为两点的中点
Affine Transformations
Affine map = linear map + translation
$$\begin{bmatrix} x'\\y' \end{bmatrix} = \begin{bmatrix} a & b\\ c & d \end{bmatrix} \begin{bmatrix} x\\y \end{bmatrix} + \begin{bmatrix} t_x\\t_y \end{bmatrix}$$Using homogeneous coordinates:
$$\begin{bmatrix} x'\\y'\\1 \end{bmatrix} = \begin{bmatrix} a & b & t_x\\ c & d & t_y\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\y\\1 \end{bmatrix}$$一些规律
- 最后一行是 $0, 0, 1$(二维情况下的仿射变换)
- 平移是最后一列
- 左上角 $2 \times 2$ 子矩阵为原来的变换矩阵
Scale
$$S(s_x, s_y) = \begin{bmatrix} s_x & 0 & 0\\ 0 & s_y & 0\\ 0 & 0 & 1 \end{bmatrix}$$Rotation
$$R(\alpha) = \begin{bmatrix} \cos \alpha & -\sin \alpha\\ \sin \alpha & \cos \alpha \end{bmatrix}$$Translation
$$T(t_x, t_y) = \begin{bmatrix} 1 & 0 & t_x\\ 0 & 1 & t_y\\ 0 & 0 & 1 \end{bmatrix}$$Composing Transform
在默认列向量情况下,变换不断左乘,变换顺序从右往左读
Decomposing Complex Transforms

以 $c$ 点为中心旋转,先平移 $-c$,绕原点旋转,再平移 $c$
$$T(c) R(\alpha) T(-c)$$
3D Transformation
同样使用齐次坐标
- 3D point = $(x, y, z, 1) ^ T$
- 3D vector = $(x, y, z, 0) ^ T$
即 $(x, y, z, w)$ 在 $w \neq 0$ 时表示点 $(x / w, y / w, z / w)$
$$\begin{bmatrix} x'\\y'\\z'\\1 \end{bmatrix}=\begin{bmatrix} a & b & c & t_x\\ d & e & f & t_y\\ g & h & i & t_z\\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x\\y\\z\\1 \end{bmatrix}$$本质是先线性变换,再平移
Rotation
绕某个轴旋转
$$R_x(\alpha) = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & \cos \alpha & -\sin \alpha & 0\\ 0 & \sin \alpha & \cos \alpha & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$$ $$R_y(\alpha) = \begin{bmatrix} \cos \alpha & 0 & \sin \alpha & 0\\ 0 & 1 & 0 & 0\\ -\sin \alpha & 0 & \cos \alpha & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$$ $$R_z(\alpha) = \begin{bmatrix} \cos \alpha & -\sin \alpha & 0 & 0\\ \sin \alpha & \cos \alpha & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$$欧拉角
$$R_{xyz}(\alpha, \beta, \gamma) = R_x(\alpha)R_y(\beta)R_z(\gamma)$$
应用:flight simulators roll, pitch, yaw
Rodrigues’ Rotation Formula
绕轴 $\vec n$ 旋转 $\alpha$,默认轴过原点
$$R(\vec n, \alpha) = \cos(\alpha) \mathrm{I} + (1 - \cos \alpha)\vec n \vec n ^ T + \sin(\alpha)\begin{bmatrix} 0 & -n_z & n_y\\ n_z & 0 & -n_x\\ -n_y & n_x & 0 \end{bmatrix}$$View / Camera transformation (视图变换)
相机
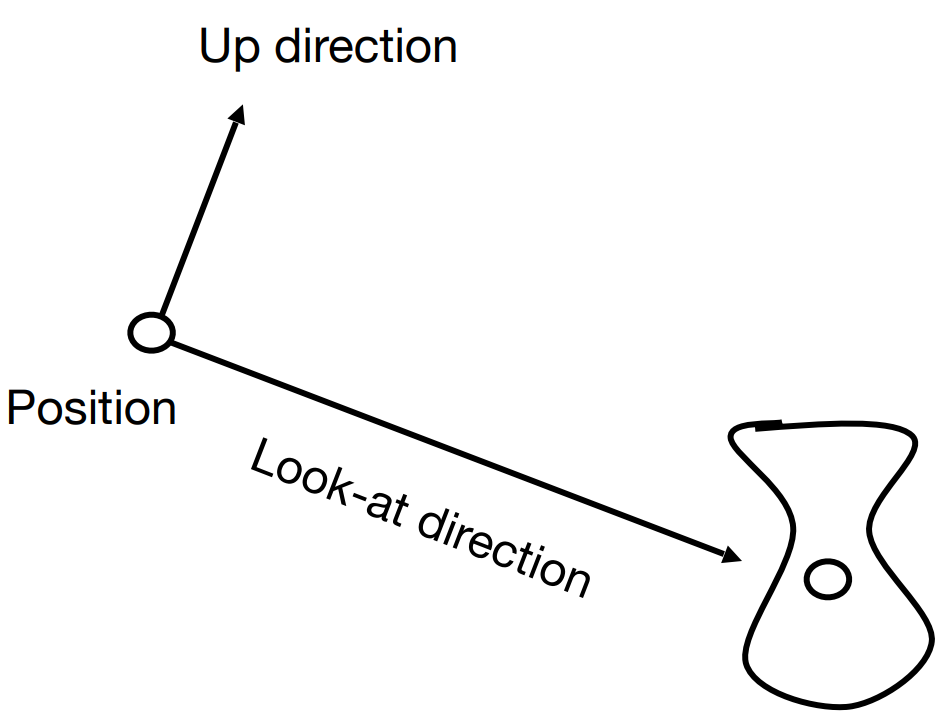
- Position $\vec e$
- Look-at $\hat{g}$
- Up direction $\hat{t}$ (与 look-at 垂直)
只要相机和物体的相对位置不变,那么最终效果就不会变,所以可将相机永远固定在原点向 $-z$ 方向看,向上是 $y$,并将物体同样移动
- 平移 $\vec{e}$ 到原点
- 旋转 $\hat{g}$ 到 $-z$
- 旋转 $\hat{t}$ 到 $y$
- 旋转 $\hat{g} \times \hat{t}$ 到 $x$
$$M_{view} = R_{view}T_{view}$$
移动 $\vec{e}$
$$T_{view} = \begin{bmatrix} 1 & 0 & 0 & -x_e\\ 0 & 1 & 0 & -y_e\\ 0 & 0 & 1 & -z_e\\ 0 & 0 & 0 & 1 \end{bmatrix}$$接下来三个旋转,考虑反过来旋转,将 $x \rightarrow \hat{g} \times \hat{t}, y \rightarrow \hat{t}, z \rightarrow -\hat{g}$,求 $R ^ {-1}_{view}$
$$R ^ {-1}_{view} = \begin{bmatrix} x_{\hat{g} \times \hat{t}} & x_{\hat{t}} & x_{-\hat{g}}& 0\\ y_{\hat{g} \times \hat{t}} & y_{\hat{t}} & y_{-\hat{g}} & 0\\ z_{\hat{g} \times \hat{t}} & z_{\hat{t}} & z_{-\hat{g}} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$$由于旋转矩阵是正交矩阵
$$R_{view} = (R ^ {-1}_{view}) ^ T = \begin{bmatrix} x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0\\ x_{\hat{t}} & y_{\hat{t}} & z_{\hat{t}} & 0\\ x_{-\hat{g}}& y_{-\hat{g}} & z_{-\hat{g}} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$$Projection transformation (投影变换)
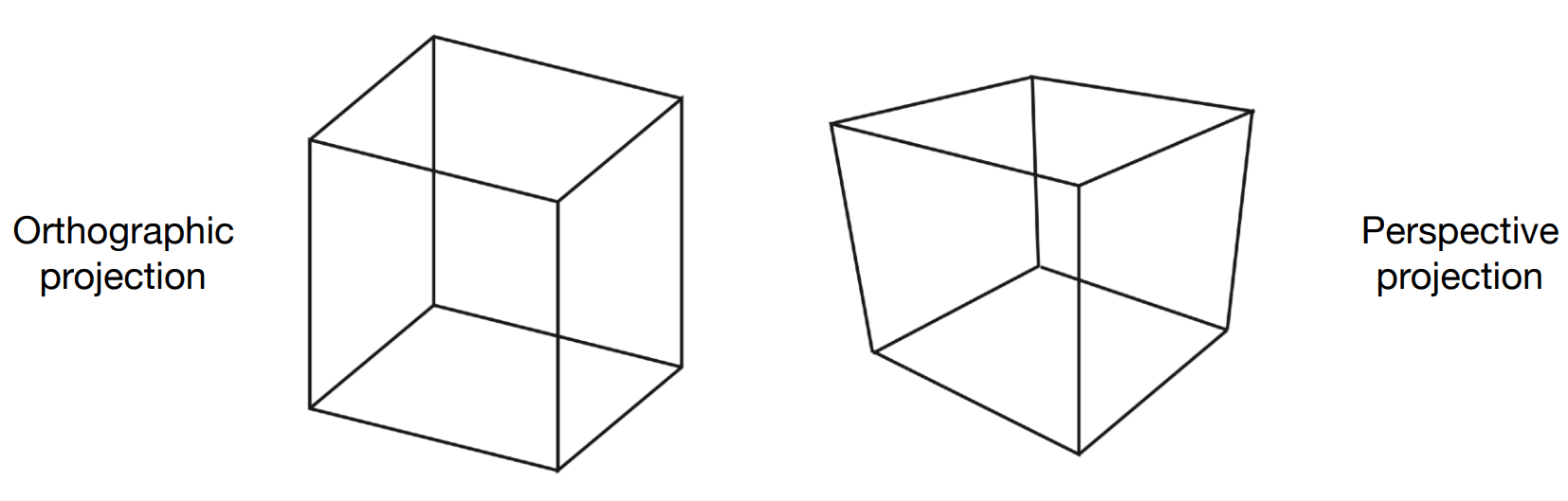
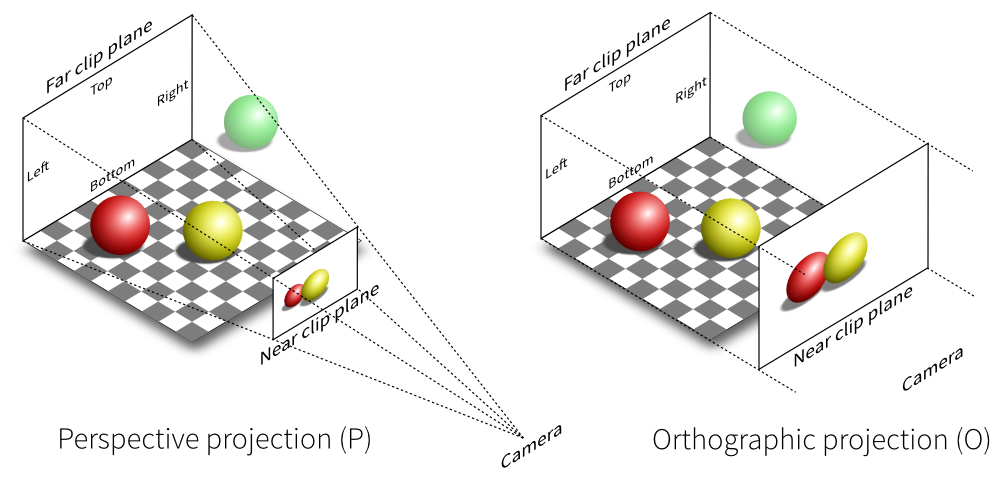
Orthographic projection (正交投影)
简单理解
- 相机放在原点上,向 $-z$ 看,向上是 $y$
- 扔掉 $z$ 坐标
- 平移缩放 $x,y$ 范围至 $[-1, 1] ^ 2$
正式做法

将 $[l, r] \times [b, t] \times [f, n]$ (视野范围) 映射到 $[-1, 1] ^ 3$ 标准 (canonical) 立方体
注:因为相机看向 $-z$,所以近 $n$ 值大于远 $f$
先平移,将中心移到原点,再缩放到 $[-1, 1] ^ 3$
$$M_{ortho} = \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & 0\\ 0 & \frac{2}{t - b} & 0 & 0\\ 0 & 0 & \frac{2}{n - f} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 & -\frac{r + l}{2}\\ 0 & 1 & 0 & -\frac{t + b}{2}\\ 0 & 0 & 1 & -\frac{n + f}{2}\\ 0 & 0 & 0 & 1 \end{bmatrix}$$Perspective projection (透视投影)
齐次坐标:$(x, y, z, 1), (kx, ky, kz, k \neq 0), (xz, yz, z ^ 2, z \neq 0)$ 都是同一个点
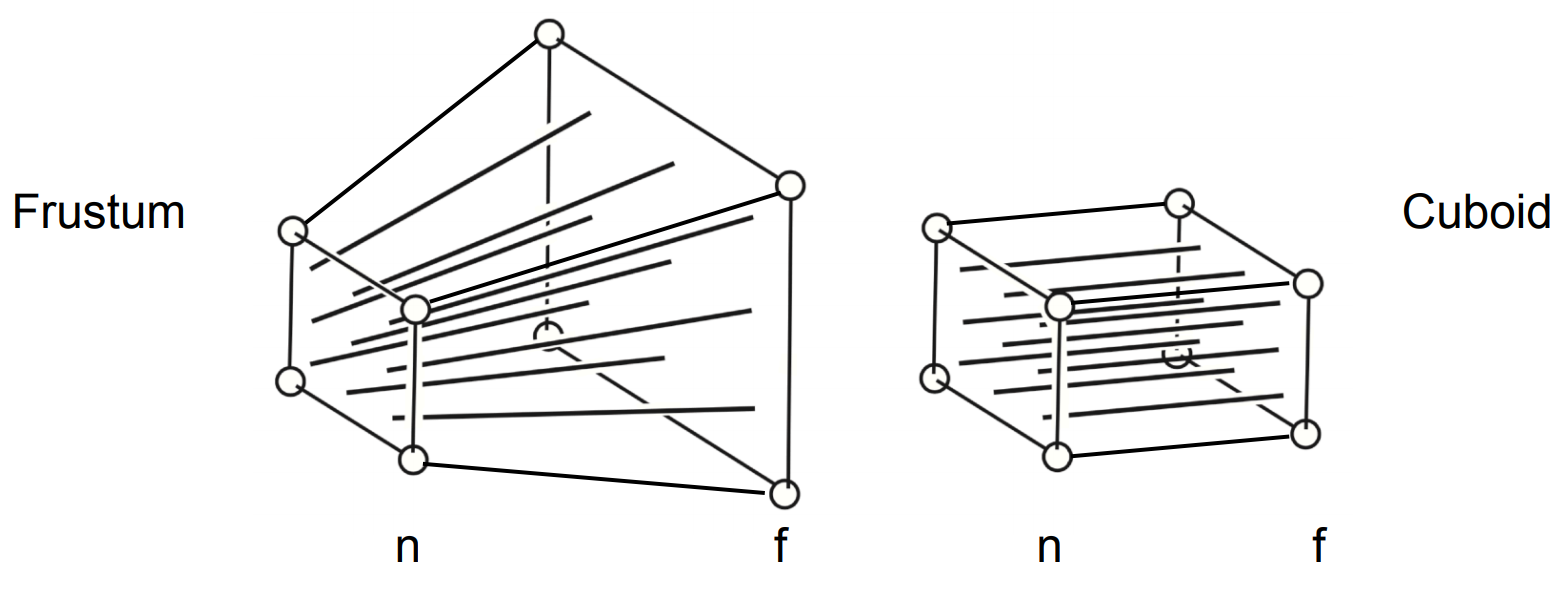
基本思路:将远平面挤压成和近平面同大小,再正交投影;近平面不会变,远平面中心点不会变
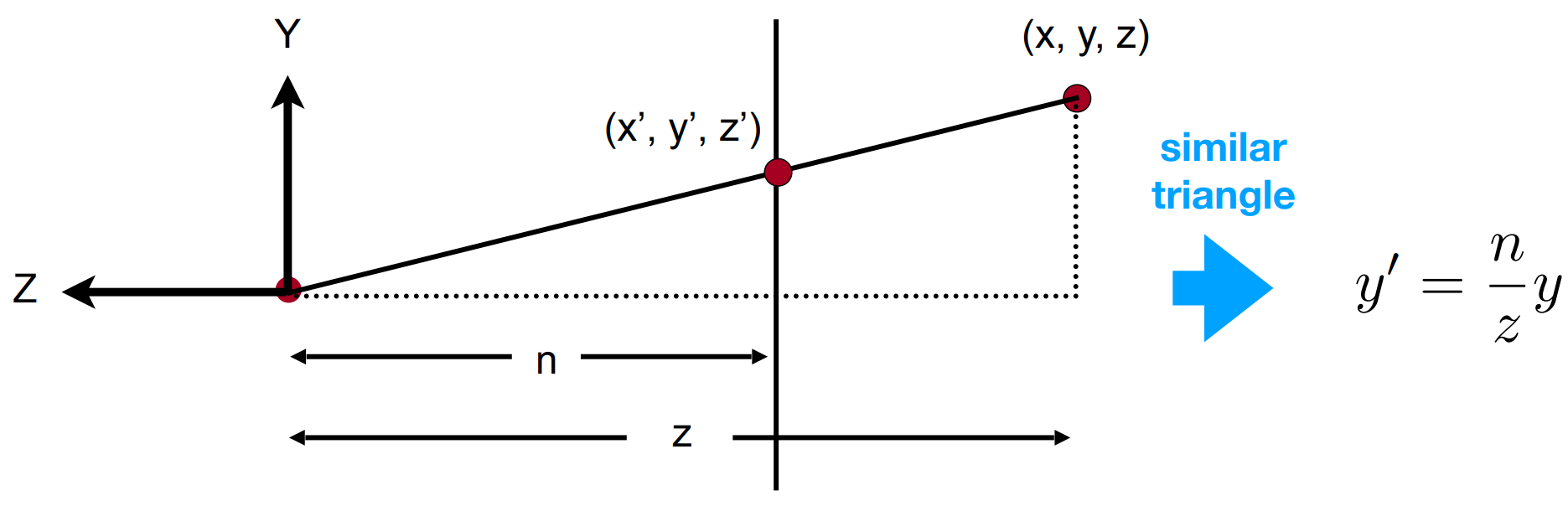
从侧面 ($x$) 看,上图右侧 $-z$ 方向即为相机看向的方向,由相似三角形可得
$$y’ = \frac{n}{z}y$$
同理
$$x’ = \frac{n}{z}x$$
所以
$$\begin{bmatrix} x\\y\\z\\1 \end{bmatrix} \Rightarrow \begin{bmatrix} nx/z\\ny/z\\\text{unknown}\\1 \end{bmatrix} = ^ {\times z}\begin{bmatrix} nx\\ny\\\text{still unknown}\\z \end{bmatrix}$$即求 $M_{persp \rightarrow ortho}$ 满足
$$M_{persp \rightarrow ortho} \begin{bmatrix} x\\y\\z\\1 \end{bmatrix}=\begin{bmatrix} nx\\ny\\\text{unknown}\\z \end{bmatrix}$$于是有
$$M_{persp \rightarrow ortho}=\begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ ? & ? & ? & ?\\ 0 & 0 & 1 & 0 \end{bmatrix}$$注意到任何一个近平面上的点不变,任何一个远平面上的点 $z$ 不会发生变化
利用近平面不变
用 $n$ 替换上面坐标变换中的 $z$,即取进平面上点 $(x, y, n, 1)$,有
对于 $M_{persp \rightarrow ortho}$ 的第三行必为 $(0, 0, A, B)$,有
$$\begin{bmatrix} 0 & 0 & A & B \end{bmatrix}\begin{bmatrix} x\\y\\n\\1 \end{bmatrix}=n^2$$即有
$$An + B = n ^ 2$$
利用远平面 $z$ 不变
取点 $(0, 0, f, 1) ^ T$,即有
于是
$$\begin{bmatrix} 0 & 0 & A & B \end{bmatrix}\begin{bmatrix} 0\\0\\f\\1 \end{bmatrix}=f^2$$即有
$$Af + B = f ^ 2$$
于是
$$\begin{cases} An + B = n ^ 2\\ Af + B = f ^ 2 \end{cases}$$所以
$$A = n + f, B = -nf$$
$$M_{persp \rightarrow ortho}=\begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n + f & -nf\\ 0 & 0 & 1 & 0 \end{bmatrix}$$最后
$$M_{persp} = M_{ortho}M_{persp \rightarrow ortho}$$
透视投影中视锥的定义 (假设 $l = -r, b = -t$)

- aspect ratio 宽高比
- field-of-view fov 垂直可视角度


